Innhold
I denne publikasjonen vil vi vurdere en av hovedsetningene i heltallsteorien – Fermats lille teoremoppkalt etter den franske matematikeren Pierre de Fermat. Vi vil også analysere et eksempel på løsning av problemet for å konsolidere det presenterte materialet.
Uttalelse av teoremet
1. Innledende
If p er et primtall a er et heltall som ikke er delelig med pderetter ap-1 - 1 dividert med p.
Det er formelt skrevet slik: ap-1 ≡ 1 (imot p).
OBS: Et primtall er et naturlig tall som bare er delelig med XNUMX og seg selv uten rest.
For eksempel:
- a = 2
- p = 5
- ap-1 - 1 = 25 - 1 - 1 = 24 – 1 = 16 – 1 = 15
- Antall 15 dividert med 5 uten en rest.
2. Alternativ
If p er et primtall, a hvilket som helst heltall, da ap sammenlignbart med a modulo p.
ap ≡ a (imot p)
Historie med å finne bevis
Pierre de Fermat formulerte teoremet i 1640, men beviste det ikke selv. Senere ble dette gjort av Gottfried Wilhelm Leibniz, en tysk filosof, logiker, matematiker, etc. Det antas at han hadde beviset allerede i 1683, selv om det aldri ble publisert. Det er bemerkelsesverdig at Leibniz oppdaget teoremet selv, uten å vite at det allerede var formulert tidligere.
Det første beviset på teoremet ble publisert i 1736, og det tilhører sveitseren, tyskeren og matematikeren og mekanikeren Leonhard Euler. Fermats lille teorem er et spesialtilfelle av Eulers teorem.
Eksempel på et problem
Finn resten av et tall 212 on 12.
Oppløsning
La oss forestille oss et tall 212 as 2⋅211.
11 er et primtall, derfor får vi ved Fermats lille teorem:
211 ≡ 2 (imot 11).
Derfor 2⋅211 ≡ 4 (imot 11).
Altså tallet 212 dividert med 12 med en rest lik 4.










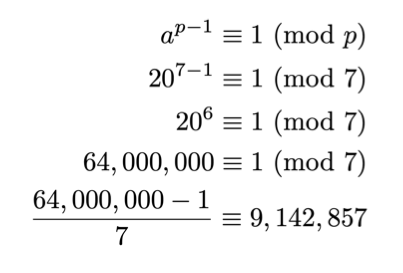
a ile p qarsiliqli sade olmalidir
+ yazilan melumatlar tam basa dusulmur. ingilis dilinden duzgun tercume olunmayib