Kryssprodukt av vektorer

I denne publikasjonen vil vi vurdere hvordan du finner kryssproduktet til to vektorer, gi en geometrisk tolkning, en algebraisk formel og egenskapene til denne handlingen, og også analysere et eksempel på løsning av problemet.

Geometrisk tolkning

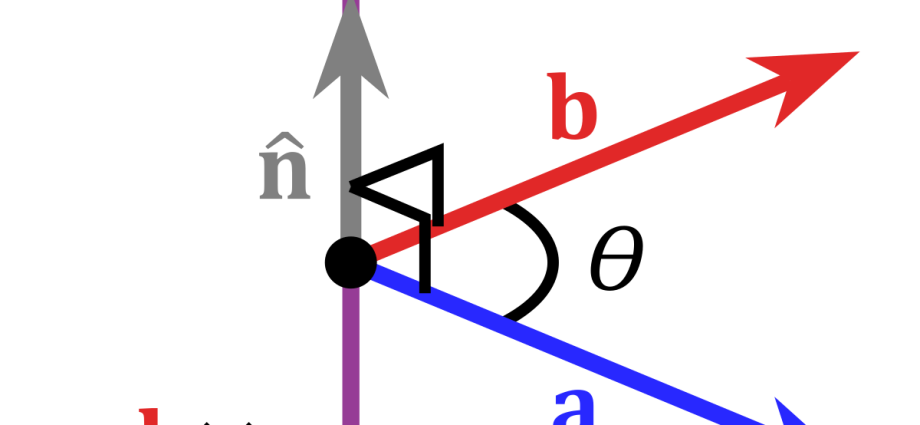
Vektorprodukt av to vektorer som ikke er null a и b er en vektor c, som er betegnet som [a, b] or a x b.

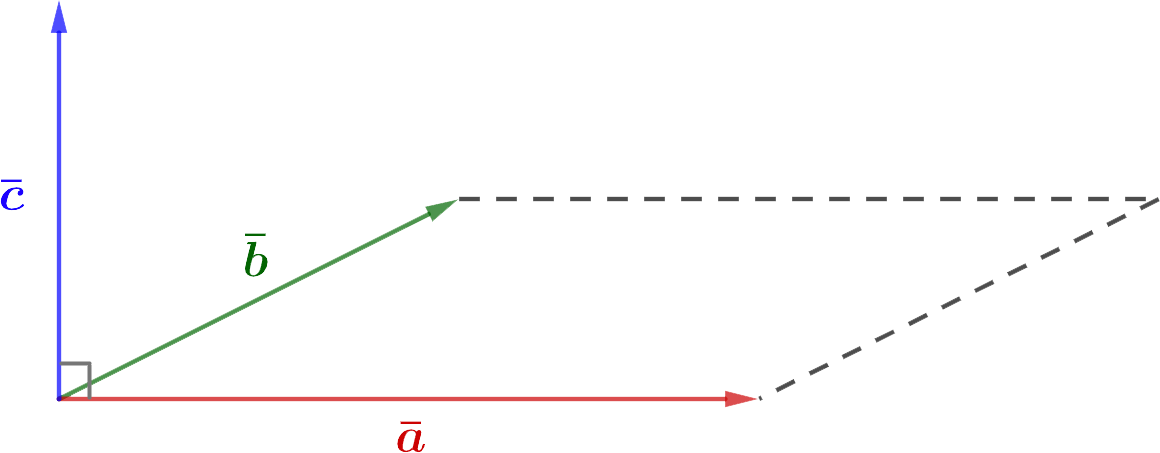
Vektorlengde c er lik arealet av parallellogrammet konstruert ved hjelp av vektorene a и b.

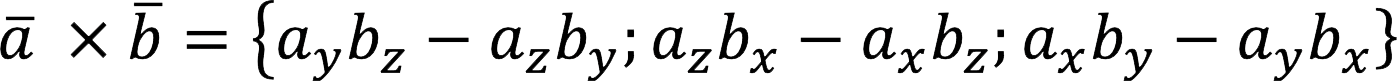
I dette tilfellet, c vinkelrett på planet de befinner seg i a и b, og er plassert slik at minst rotasjon fra a к b ble utført mot klokken (fra enden av vektoren).

Kryssproduktformel

Produkt av vektorer a = {a_x; til_y,_z} Jeg b = {b_x; b_y, b_z} beregnes ved å bruke en av formlene nedenfor:

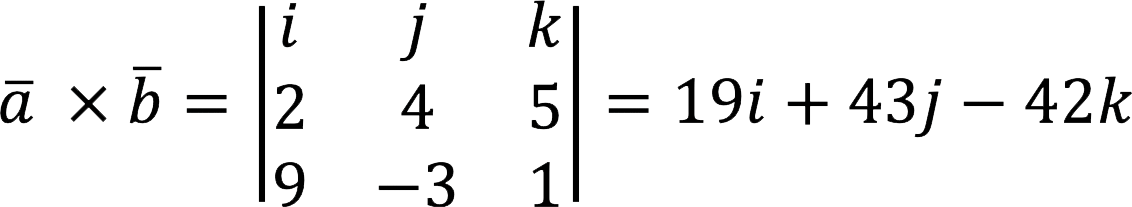
Kryss produktegenskaper

1. Kryssproduktet av to ikke-null vektorer er lik null hvis og bare hvis disse vektorene er kollineære.

[a, b] = 0, Hvis a || b.

2. Modulen til kryssproduktet av to vektorer er lik arealet av parallellogrammet dannet av disse vektorene.

S_parallelt = |a x b|

3. Arealet av en trekant dannet av to vektorer er lik halvparten av deres vektorprodukt.

S_Δ = ¹/₂ · |a x b|

4. En vektor som er et kryssprodukt av to andre vektorer er vinkelrett på dem.

c ⟂ a, c ⟂ b.

5. a x b = -b x a

6. (m a) x a = a x (m b) = m (a x b)

7. (a + b) x c = a x c + b x c

Eksempel på et problem

Beregn kryssproduktet a = {2; 4; 5} и b = {9; -to; 3}.

Beslutning:

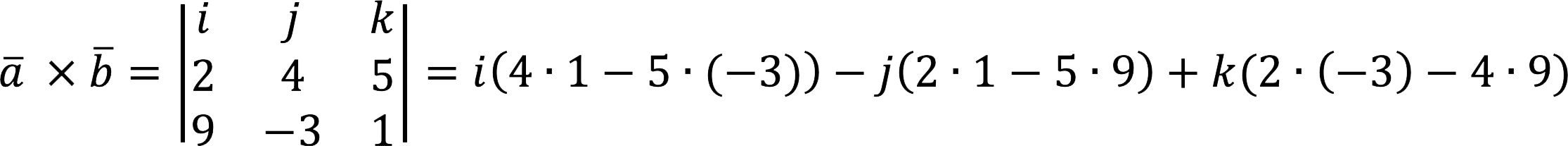
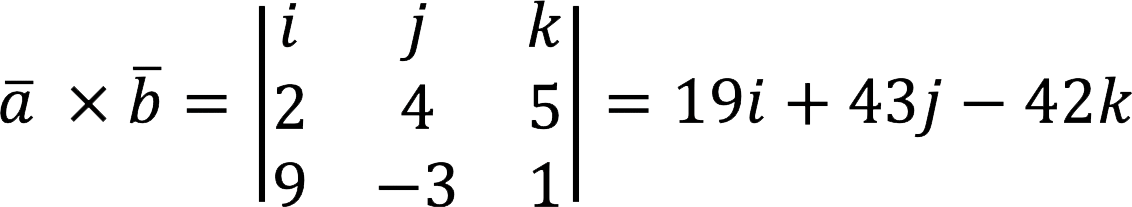
Svar: a x b = {19; 43; -42}.